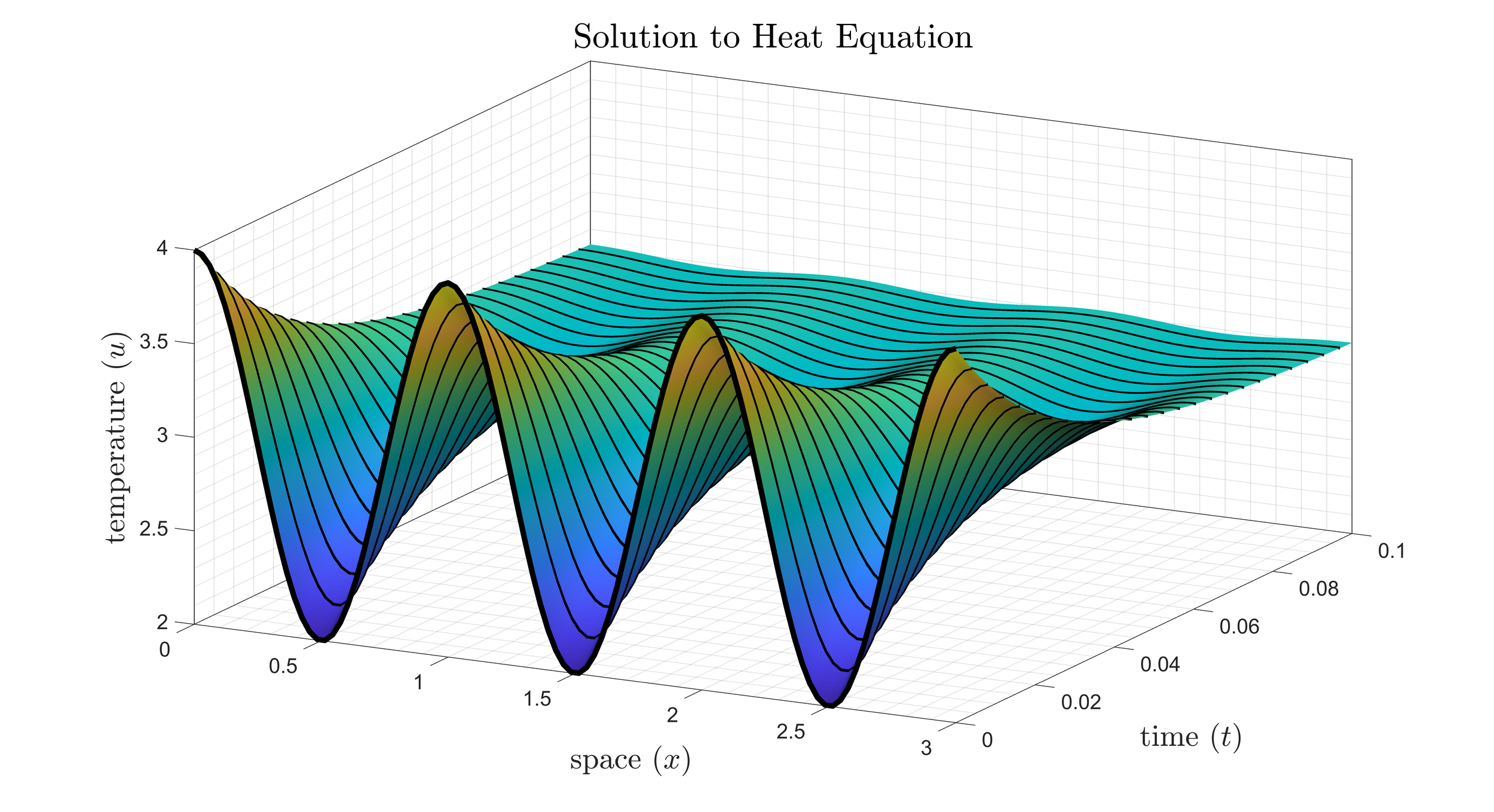
This course is an introduction to the theory of and solutions to partial differential equations. The three big PDEs are the motivation: the heat equation, the wave equation, and Laplace’s equation. A solid understanding of linear systems of IVPs is assumed, and a strong focus on BVPs and Cauchy-Euler problems is applied initially. The theory and application of Fourier Series is motivated by finding the solutions to the three PDEs with Dirichlet and/or Neumann boundary conditions. Solutions of nonhomogeneous PDES on finite domains are considered as well as integral transforms for semi-infinite and infinite domain problems. Other topics include the method of characteristics, existence theorems, and Green’s Functions. The figure depicts the solution to the heat equation with no flux boundary conditions.