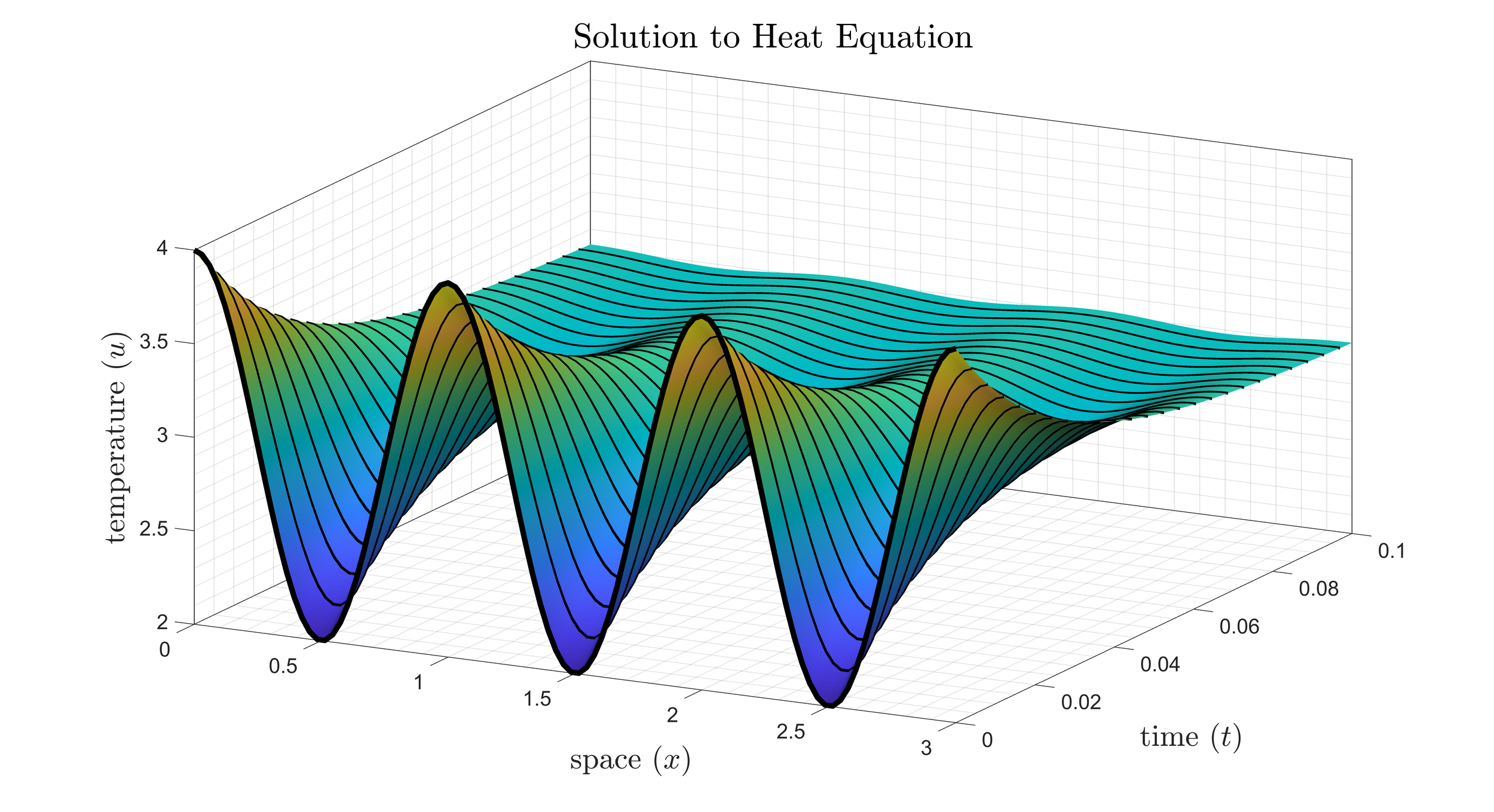
MAT 473 -- Partial Differential Equations
This course is an introduction to the theory of and solutions to partial differential equations. The three big PDEs are the motivation: the heat equation, the wave equation, and Laplace’s equation. A solid understanding of linear systems of IVPs is assumed, and a strong focus on BVPs and Cauchy-Euler problems is applied initially. The theory and application of Fourier Series is motivated by finding the solutions to the three PDEs with Dirichlet and/or Neumann boundary conditions. Solutions of nonhomogeneous PDES on finite domains are considered as well as integral transforms for semi-infinite and infinite domain problems. Other topics include the method of characteristics, existence theorems, and Green’s Functions. The figure depicts the solution to the heat equation with no flux boundary conditions.
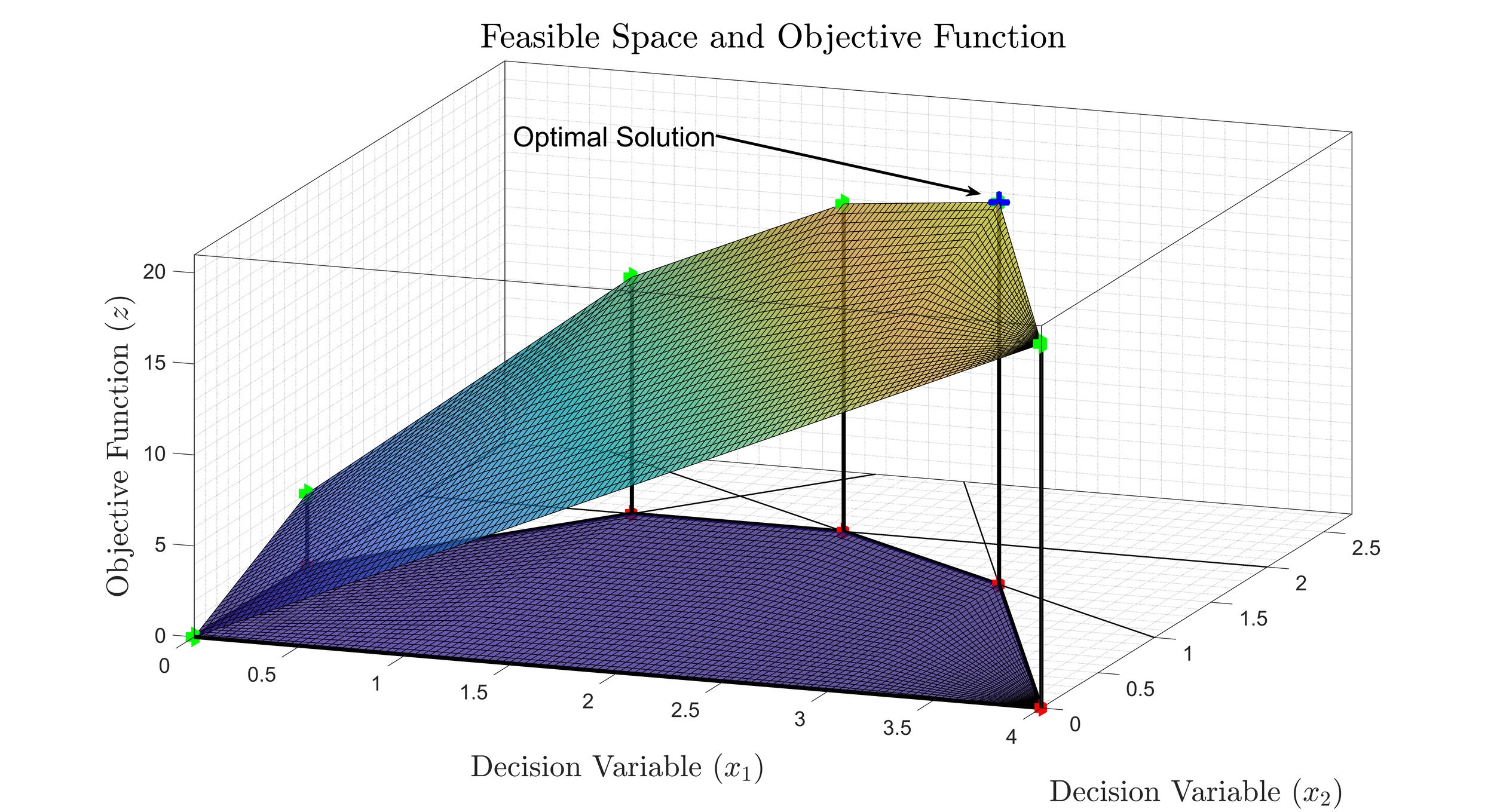
MAT 361 -- Operations Research
Operations Research is a classic study of mathematical optimization and its applications to a wide array of real-world problems. Operations Research uses quantitative methods to determine the best decision for an operating system. A mathematical approach to studying methods as applied to the decision process in industry is taken. The methods studied are selected from among: linear programming, game theory, graph theory and network analysis. Our focus in this course will be on linear programming and sensitivity analysis. Students will be required to use appropriate computer software, including Excel. The figure depicts the optimal solution to a two-dimensional linear programming problem. The planar surface shows the objective function reaching it’s maximum value at a corner point of the feasible space.
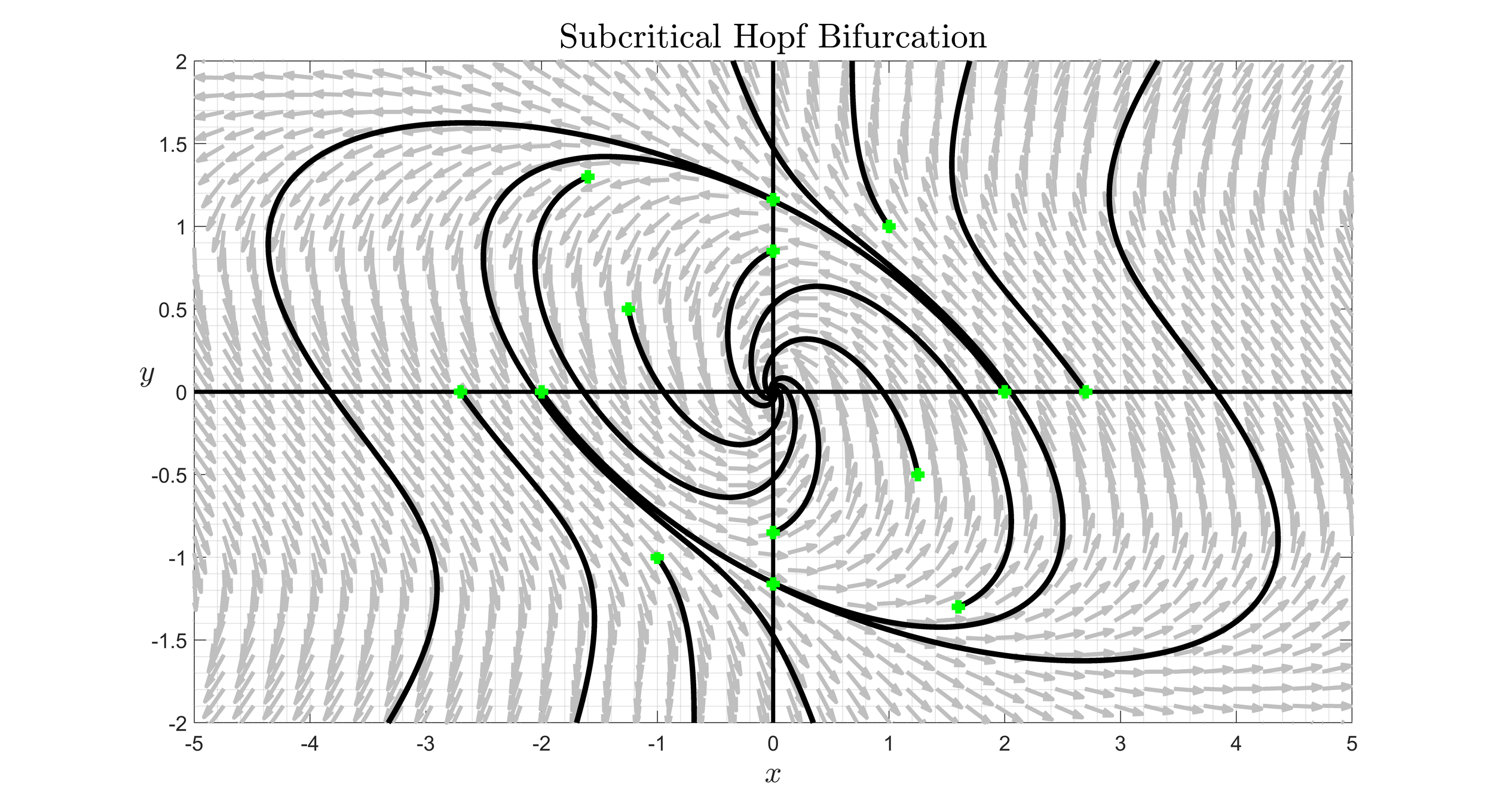
MAT 340 -- Differential Equations
An introduction to the theory of ordinary differential equations and their applications. Topics include analytical and qualitative methods for analyzing first-order differential equations, second-order differential equations, and systems of differential equations with an emphasis on modeling predator-prey and competing species systems. Analytical methods for finding solutions to differential equations will range from separation of variables and variation of parameters to Laplace transforms. Special emphasis will be placed on equilibria, stability analysis, and phase portraits of both linear and nonlinear equations and systems. The figure shows the phase-portrait with several trajectories of a nonlinear system that undergoes a subcritical Hopf bifurcation.

MAT 182 -- Calculus II
This course is one of a series intended for students who major in mathematics, the sciences, or engineering. The topics include the definition, properties, and applications of definite integrals; properties, derivatives, and integrals of exponential, logarithmic, trigonometric, inverse trigonometric, and hyperbolic functions with applications; techniques of integration; indeterminate forms and improper integrals; sequences, series, and convergence tests; differentiation and integration of power series; and polar integrals. This figure shows the function f(x) = cos(x) along with several approximating Taylor polynomials centered at a = pi/3. We can see that as the degree of the polynomial gets larger, the Taylor polynomials converge to the function.
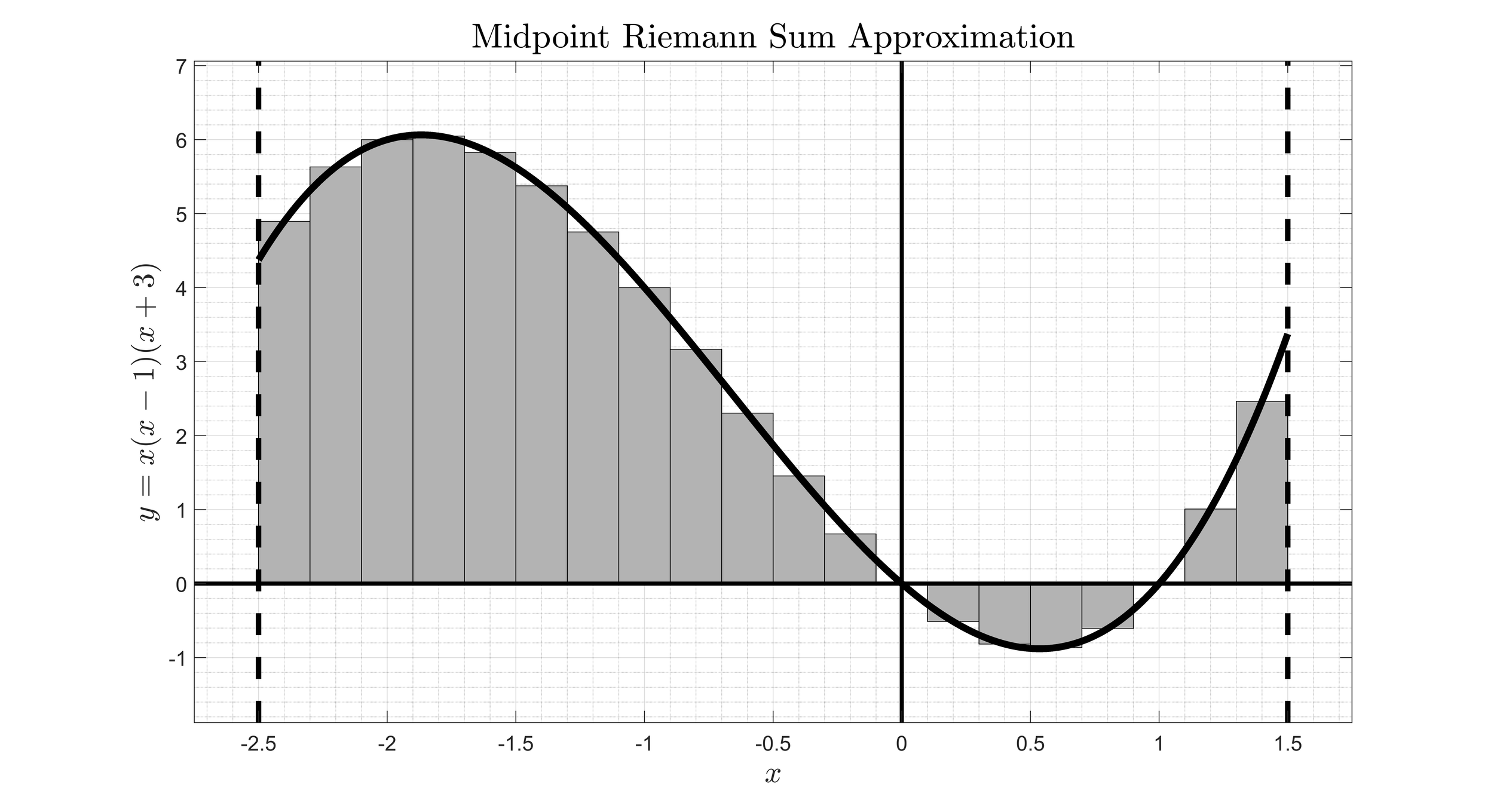
MAT 181 -- Calculus
This course is one of a series intended for students who major in mathematics, the sciences, or engineering. The topics include the definition and calculation of limits, continuity and differentiability, differentials, derivatives of algebraic and transcendental functions, the application of derivatives to graphing, antiderivatives, and the introduction of the definite integral, applications of definite integrals; and some techniques of integration. The figure above shows a midpoint Riemann sum approximation to the area under the curve y = x(x-1)(x+3).
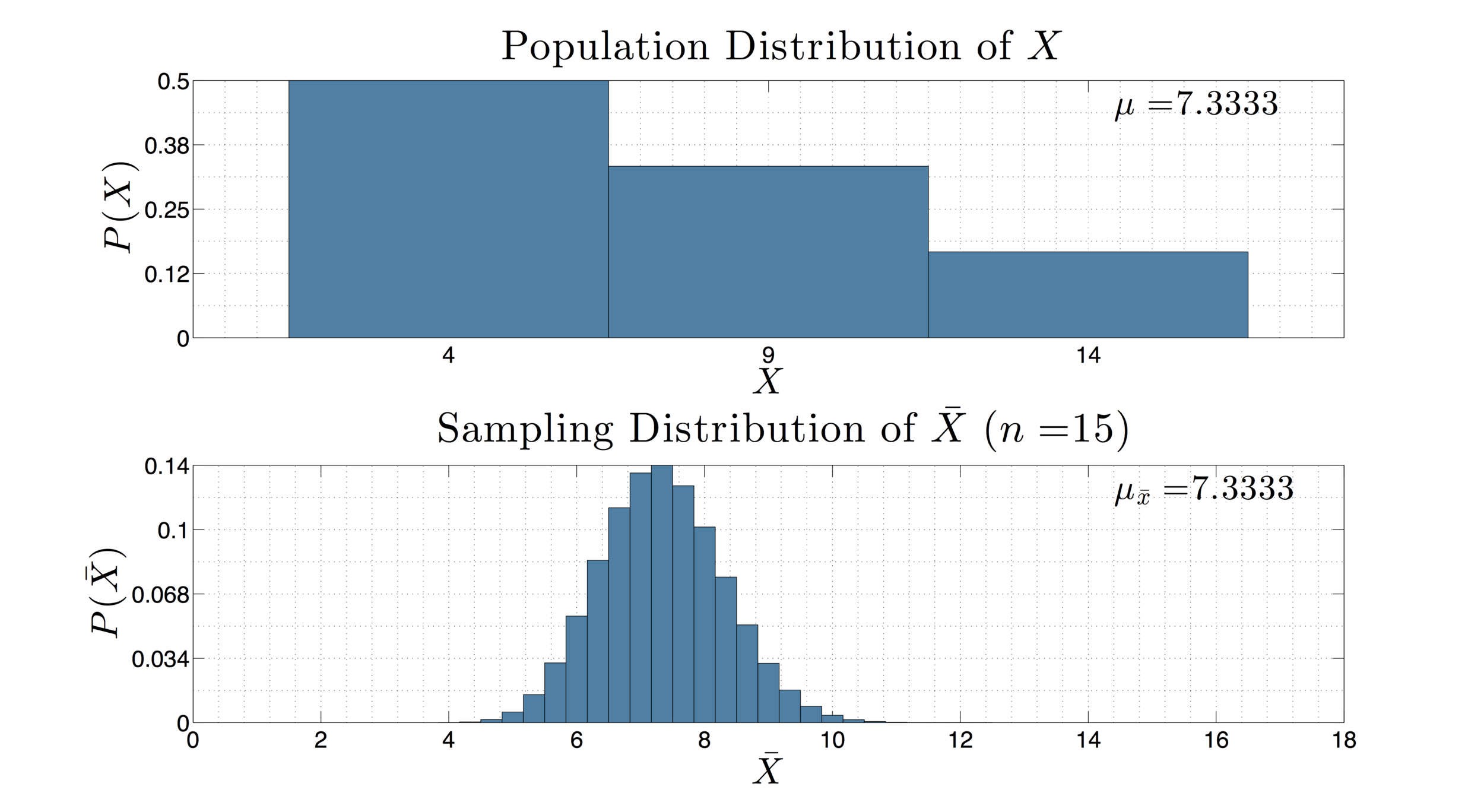
MAT 140 -- Applied Statistical Methods
This course is an introduction to quantitative methods as applied to statistical reporting and data analysis. It incorporates some or all of the following: Techniques for obtaining, analyzing and presenting data in numerical form; measures of central tendency and dispersion; the normal distribution curve; standard scores; applicability of probability and sampling theory to statistical research; interpretation of confidence intervals; hypothesis testing; correlation; linear regression. The figure to the left gives a simple population distribution and the corresponding sampling distribution of sample means from samples of size 15.
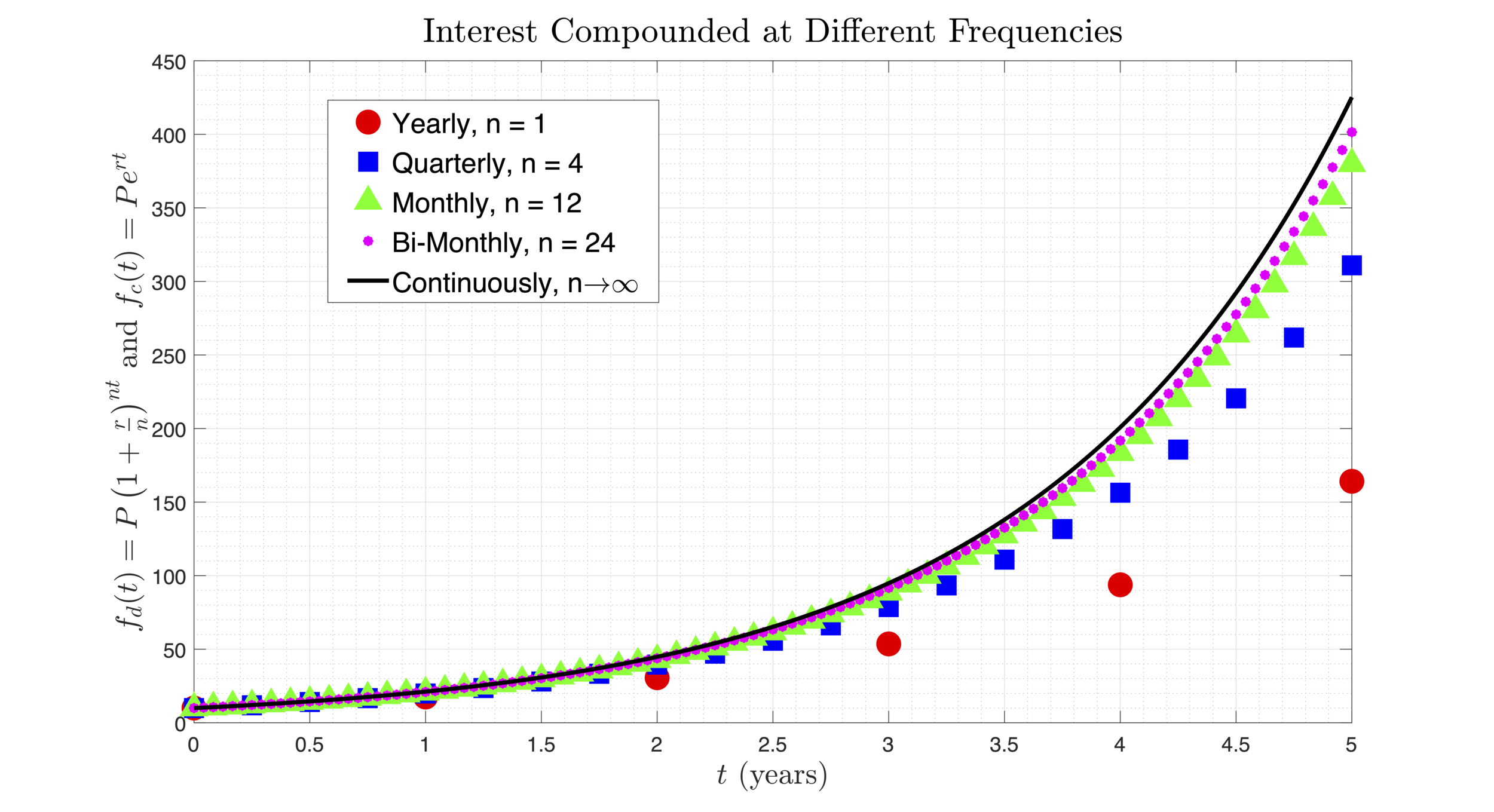
MAT 115 -- Precalculus
This course is designed to give students a thorough review of the mathematics background needed for calculus courses. Topics generally include properties of the real numbers, problem-solving using equations and inequalities, algebraic functions, graphing, and systems of equations. A treatment of trigonometry is also provided as well as applications of exponential functions. The figure shows trajectories of different exponential functions. Each function produces the amount of money at time t in an account if yearly interest is compounded n times throughout the year. The black curve shows the limit as n -> infinity, which indicates that interest is compounded continuously.
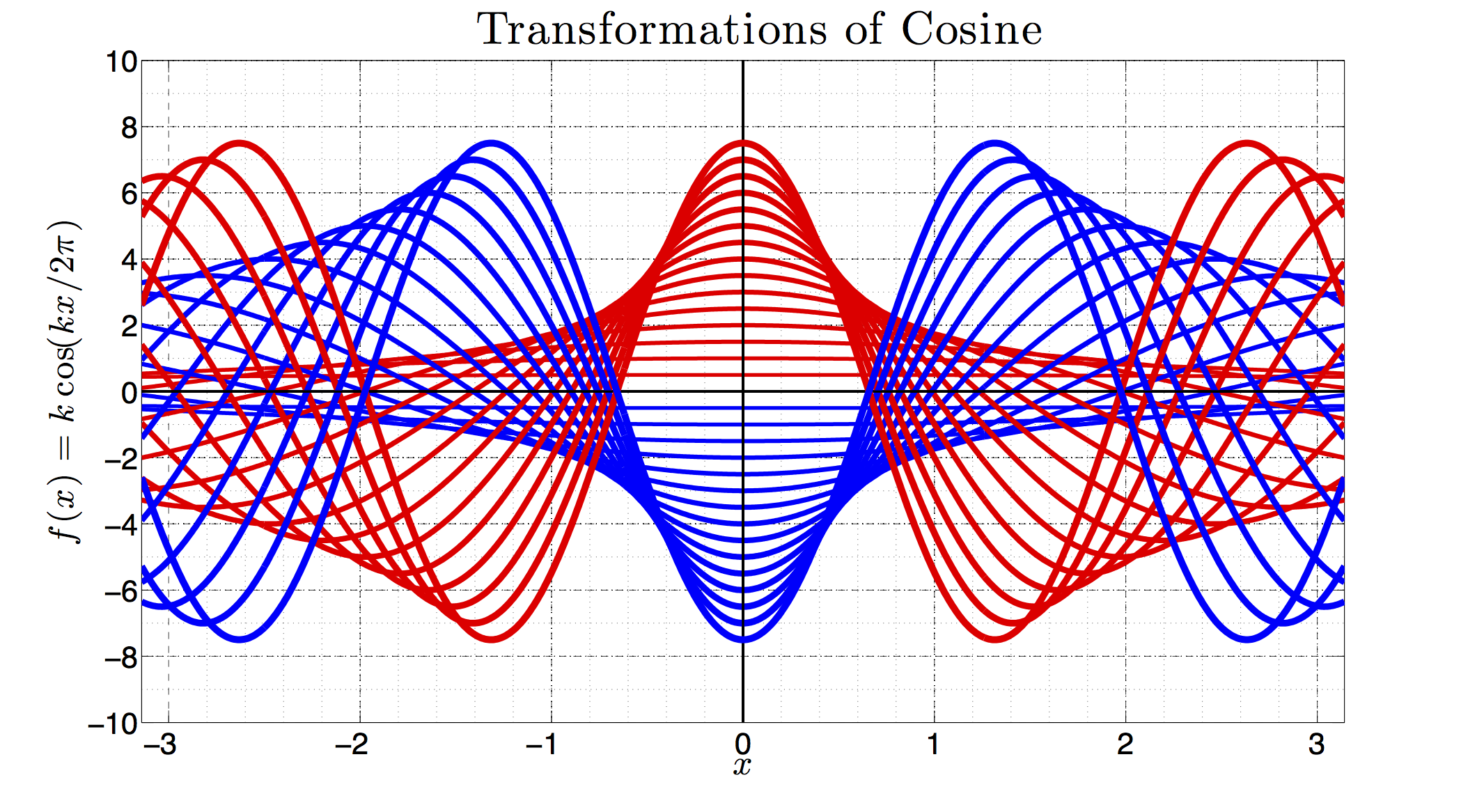
MAT 106 -- Trigonometry
This course is intended for students with an elementary knowledge of algebra who need more work in trigonometric topics before taking more advanced mathematics courses. Topics include properties of and operations of functions, inverse functions, exponential and logarithmic functions, angle measurement, trigonometric functions and their inverses, graphing functions, and problem solving with equations. The figure shows the graph of the cosine function for increasing amplitude and increasing frequency given by f(x) = kcos(kx/2pi), for k ranging from -15 to 15.







